می دانید تفاوت موفق ترین شرط بندان با بقیه در چیست؟ شاید فکر کنید به خاطر دانش بالا یا مهارت فوق العاده شان در پیش بینی است. شاید به نظرتان به خاطر خوب بودن کارشان با اعداد یا انتخاب مستمر بهترین استراتژی ها است. سلسله مطالب روانشناسی شرط بندی را از دست ندهید. این قسمت در ارتباط با ارزش مورد انتظار صحبت خواهیم کرد.
مقدمه
برای برد در شرط بندی ورزشی، استراتژی مدنظرتان باید ارزش مورد انتظار مثبت داشته باشد که می تواند شامل تخمین میانگین بردتان برای هر شرط باشد. حالا، برای رسیدن به حداکثر سود، چه میزان سرمایه باید وسط بگذارید؟ برای پی بردن به پاسخ این سوال، باید مفهوم سودمندی (Utility) را درک کنید.
ارزش مورد انتظار (Expected Value)، که در ابتدا در قرن 17 ام و از سوی ریاضی دانان فرانسوی پاسکال و فرمت در تلاش برای حل مساله ای در خصوص بازی امتیازات، مورد مکاشفه قرار گرفت، نشان می دهد باید به طور میانگین از یک شرط به چه میزان انتظار برد داشته باشیم. با این حال، داده چندانی در مورد میزان سرمایه ای که شرط بند برای هر شرط باید اختصاصی دهد، ارائه نشده است. اینجا است که سودمندی مورد انتظار (Expected Utility) وارد میدان می شود.
- بیشتر بخوانید: ارزش مورد انتظار در پوکر چیست؟
تشریح ارزش مورد انتظار و سودمندی مورد انتظار
ارزش مورد انتظار (EV)، در شرط بندی از طریق ضرب احتمال بردتان با مبلغی که ممکن است از هر شرط ببرید و کسر احتمال باخت ضرب در مبلغ از دست رفته در هر شرط، به دست می آید. چون احتمال باخت برابر با یک یا 100 درصد منهای احتمال برد است، به فرمول ساده زیر می رسیم:
EV= po-1
حرف O نشانگر ضریبی است که توسط بوک میکر (نهاد شرط بندی مربوط) تعیین شده است. ارزش مورد انتظار، مهم ترین عدد برای هر شرط بندی است، چون مشخص می کند فرد در بلند مدت پول به دست می آورد یا از دست می دهد. فرد بعد از محاسبه EV، باید تصمیم بگیرد چقدر پول در شرط بگذارد. ریاضی دان قرن 18 ام، دنیل برنولی به این نتیجه رسید که تنها افراد ناآگاه می توانند صرفا با در نظر گرفتن معیار بی طرفانه EV و صرف نظر از معیارهای انسانی، اقدام به تصمیم در خصوص میزان سرمایه هر شرط کنند. این معیار انسانی شامل اشتیاق برای برد (یا باخت) مبلغ مورد نظر است که از آن به عنوان سودمندی یاد می شود.
سودمندی و ابهام
دو صندوق مقابلتان قرار دارد. اولی 10 هزار دلار پول نقد در خود دارد. دومی 20 هزار دلار پول نقد به خود می بیند یا خالی است. نمی دانیم در صندوق دوم چیست، ولی احتمال هر دو گزینه وجود دارد. از شما خواسته می شود یکی از دو صندوق را انتخاب کنید. روی کدام یک دست می گذارید؟
این یکی از قدیمی ترین معماهای سودمندی به حساب می رود. از لحاظ ریاضی، هر دو صندوق ارزش مورد انتظار یکسانی دارند که 10 هزار دلار است. اگر بتوانید بارها و بارها از بین دو صندوق انتخاب کنید، مهم نیست کدام یک را برمی دارید، چون در نهایت پول یکسانی به دست می آورید. با این حال، فقط یک بار می توانید این بازی را انجام دهید. از این رو، قانون اعداد بزرگ که قبلا در خصوص آن صحبت کردیم، اینجا کارگر نخواهد بود.
کدام صندوق؟
اگر صندوق اول را بردارید، مطمئن هستید 10 هزار دلار به جیب می زنید. اگر دومی را انتخاب کنید، جایزهتان بسته به شانس خواهد بود. اگر خوش شانس باشید، 20 هزار دلار ثروتمندتر می شوید. اگر هم بدشانسی بیاورید، چیزی دستتان را نخواهد گرفت. همان طور که قابل انتظار است، خیلی ها با انتخاب صندوق اول، گزینه مطمئن تر را ترجیح می دهند.
از جنبه سودمندی، اطمینان به صندوق 10 هزار دلار خیلی بالاتر از به ریسک گذاشتن همه چیز برای پی بردن به محتویات صندوق دوم است. کسانی که این گزینه را انتخاب می کنند، سودمندی را به قمار با وجود ارزش مورد انتظار یکسان، ترجیح می دهند.
چطور میزان ایده آل مبلغ هر شرط را مشخص کنیم؟
دنیل برنولی به این نتیجه رسید که علت رفتار عاقلانه خیلی از افراد موقع تصمیم گیری با تکیه بر اطمینان، خطرگریزی (Risk Aversion) است. او در این باره نوشته است: «سودمندی حاصل از هرگونه افزایش اندک ثروت با مقدار دارایی تحت اختیار قبلی متناسب خواهد بود.» به بیان دیگر، هر چه ثروت بیشتری از قبل داشته باشید، سودمندی مورد انتظارتان در موارد مختلف، کمتر می شود. این کاربرد سودمندی شکل لگاریتمی دارد و معمولا به عنوان سودمندی حاشیه ای ثروت کاهشی شناخته می شود.
از جمله کاربردهای بسیار رایج نظریه های برنولی، می توان به پلن مدیریت سرمایه ای که شرط بندان آن را به نام کلی کرایتریون می شناسند، اشاره کرد. این پلن در حالی که جان کلی در سال 1956 در حال کار بر روی حله مساله مربوط به نویز تماس های های تلفنی مسافت دور، بود، به دست آمد. بلافاصله هم از سوی سرمایه گذاران و شرط بندان به عنوان ابزاری برای ایده آل سازی مدیریت پول و افزایش سرمایه، مورد استفاده قرار گرفت.
در حالی که انگیزه کلی کاملا از برنولی متفاوت بود، معیار ارائه شده از سوی او، کاملا با کاربرد لگاریتمی برنولی، منطبق بود. این فرمول سبب می شود شرط بندان دقیقا مقداری از پول خود را به ریسک بگذارند که هم با EV متناسب است و هم با احتمال برد، تناسب دارد.
با یادآوری دوباره فرمول EV که در آن، P نشانه احتمال موفقیت و O نشانه ضریب ارائه شده از سوی بوک میکر است، فرمول کلی کرایتریون به شکل زیر ارائه می شود:
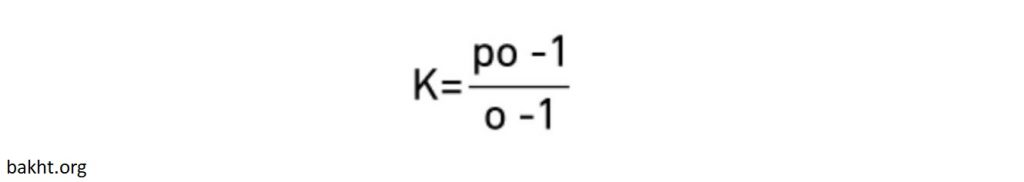
فرمول کلی کرایتریون، سودمندی لگاریتمی مورد انتظار را به حداکثر می رساند. اگر از این فرمول استفاده کنید، سود کسب شده شما حتما بیشتر می شود، ولی برای استفاده از آن، حتما باید تخمین دقیقی از نتیجه احتمالات داشته باشید.
نتیجه گیری
استفاده از رویکرد کلی، باعث می شود میزان برد شرط بندان در بلندمدت به حداکثر برسد. با این حال، برای استفاده از این فرمول، باید بوک میکری پیدا کنید که به استراتژی های همیشگی موفقیت مشکوک نشود و به دلیل برد مستمر، فعالیتتان را محدود نکند!






دیدگاهتان را بنویسید