توزیع پواسون در کنار داده های تاریخی، یک متد ساده و قابل اعتماد برای محاسبه محتمل ترین نتیجه در یک بازی فوتبال است که می توان از آن در شرط بندی استفاده کرد. در این یادداشت به شما نشان می دهیم چطور محاسبات قدرت هجومی-دفاعی لازم را حساب کنید و با یک میانبر به ارزش های توزیع پواسون برسید. بدین ترتیب شما می توانید به کمک توزیع پواسون نتیجه بازی های فوتبال را پیش بینی کنید.
توزیع پواسون یک مفهوم ریاضی برای تبدیل میانگین متوسط به احتمال وقوع متغیر در یک توزیع است. به عنوان مثال، اگر ما می دانیم که تیم منچسترسیتی به طور میانگین در هر بازی اش 1.7 گل به ثمر می رساند، می توانیم با استفاده از فرمول توزیع پواسون به این نقطه برسیم: این میانگین مساوی است با صفر گل زدن سیتی در 18.3 درصد بازی ها، 1 گل زدن سیتی در 31 درصد از بازی ها، 2 گل زدن سیتی در 26.4 درصد از بازی ها و 3 گل زدن سیتی در 15 درصد از بازی ها.
توزیع پواسون؛ محاسبه احتمالات وقوع نتیجه
قبل از اینکه از پواسون برای محاسبه محتمل ترین نتیجه یک بازی استفاده کنیم، ما باید تعداد میانگین گل ها درهر تیم را حساب کنیم تا احتمال گلزنی شان در آن دیدار مشخص شود. برای محاسبه این مورد هم باید از قدرت هجومی و قدرت دفاعی هر تیم و مقایسه آن ها استفاده کنیم.
وقتی که می خواهیم قدرت هجومی و قدرت دفاعی را حساب کنیم، انتخاب یک طیف داده نماینده خیلی مهم است. اگر زیادی طولانی باشد داده موردنظر به قدرت فعلی تیم ربطی نخواهد داشت. اگر زیادی کوتاه باشد به داده های پرت اجازه می دهد داده اصلی را منحرف کنند. 38 بازی انجام شده هر تیم در فصل 2015-2016 لیگ برتر انگلیس یک نمونه کافی برای اجرای توزیع پواسون است.
چگونگی محاسبه قدرت هجومی
اولین قدم در محاسبه قدرت هجومی براساس نتایج فصل گذشته این است که تعداد میانگین گل های زده هر تیم را در هر بازی خانگی و در هر بازی خارج از خانه مشخص کنیم.
برای محاسبه این مورد باید تعداد کل گل های زده در فصل گذشته را بر تعداد بازی های انجام شده تقسیم کنیم:
مجموع گل های زده در خانه در یک فصل تقسیم بر تعداد بازی ها در یک فصل
مجموع گل های زده در خارج از خانه در یک فصل تقسیم بر تعداد بازی ها در یک فصل
در فصل 2015-2016 لیگ برتر انگلیس 567/380 گل در خانه و 459/380 گل در خارج از خانه زده شده و این یعنی به طور میانگین 1.492 گل در هر بازی خانگی و 1.207 گل در هر بازی خارج از خانه.
تعداد میانگین گل های زده در خانه: 1.492
تعداد میانگین گل های زده در خارج از خانه: 1.207
نسبت میانگین یک تیم و میانگین لیگ هم قدرت هجومی را نشان می دهد.
چگونگی محاسبه قدرت دفاعی
ما همچنین باید تعداد میانگین گل های خورده یک تیم متوسط را حساب کنیم. این روش هم برعکس روش قبلی است (تعداد گل هایی که یک تیم میزبان می زند برابر با همان تعدادی است که یک تیم میهمان دریافت می کند):
تعداد میانگین گل های خورده در خانه: 1.207
تعداد میانگین گل ها خورده در خارج از خانه: 1.492
نسبت میانگین یک تیم و میانگین لیگ هم قدرت دفاعی را نشان می دهد.
حالا می توانیم از این اعداد برای محاسبه قدرت هجومی و قدرت دفاعی دو تیم تاتنهام و اورتون استفاده کنیم (از روز 1 مارس سال 2017).
پیش بینی گل های تاتنهام

محاسبه قدرت هجومی تاتنهام:
- قدم اول: تعداد گل های زده در خانه تیم میزبان (تاتنهام: 35) در فصل گذشته را بر تعداد بازی های خانگی تقسیم می کنیم (35/19): 1.842.
- قدم دوم: این عدد را بر تعداد میانگین گل های زده در خانه (در هر بازی یک فصل) تقسیم می کنیم (1.842/1.492) و به قدرت هجومی می رسیم: 1.235.

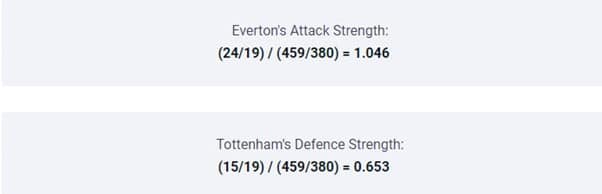
محاسبه قدرت دفاعی اورتون:
- قدم اول: تعداد گل های خورده در بازی های خارج از خانه تیم میهمان (اورتون: 25) در فصل گذشته را بر تعداد بازی های خارج از خانه تقسیم می کنیم (25/19): 1.315.
- قدم دوم: این عدد را بر تعداد میانگین گل های خورده یک تیم خارج از خانه (در هر بازی از یک فصل) تقسیم می کنیم (1.315/1.492) و به قدرت دفاعی می رسیم: 0.881.

حالا می توانیم از فرمول زیر برای محاسبه تعداد محتمل گل های زده تاتنهام استفاده کنیم (برای این کار باید قدرت هجومی تاتنهام را در قدرت دفاعی اورتون و تعداد میانگین گل های در خانه در لیگ برتر ضرب کنیم):
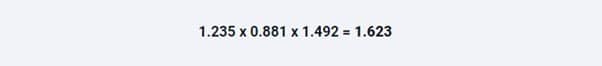
پیش بینی گل های اورتون
برای محاسبه تعداد گل های زده محتمل اورتون، باید از فرمول های بالا استفاده کنیم ولی به جای تعداد میانگین گل ها در خانه، تعداد میانگین گل ها در خارج از خانه را بنویسیم.
به همین ترتیبی که ما تعداد گل های زده تاتنهام را پیش بینی کردیم، ما می توانیم تعداد گل های زده محتمل اورتون را حساب کنیم (برای این کار باید قدرت هجومی اورتون را در قدرت دفاعی تاتنهام و تعداد میانگین گل های خارج از خانه در لیگ برتر ضرب کنیم).
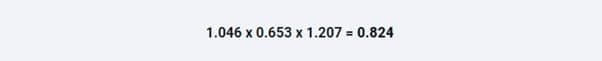
توزیع پواسون؛ پیش بینی نتایج چندگانه
طبیعتا هیچ بازی فوتبالی با نتیجه 1.623-0.824 به پایان نمی رسد. این فقط یک عدد میانگین است. توزیع پواسون فرمولی است که توسط ریاضی دان فرانسوی، سیمئون دنیس پواسون ایجاد شده است و به ما کمک می کند از این اعداد برای توزیع 100 درصد احتمال در یک طیف از گل ها برای هر تیم استفاده کنیم.

البته می توانیم از ابزارهای آنلاین مثل Poisson Distribution Calculator استفاده کنیم که بخش زیادی از معادله را به جای ما انجام دهد.
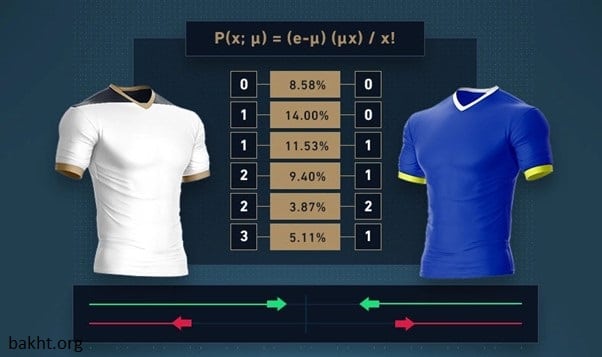
تنها چیزی که لازم داریم وارد کردن رویدادهای متفاوت (اینجا گل ها از صفر تا 5) و اتفاقات مورد انتظار است که احتمال گلزنی هر کدام از تیم هاست (در مثال ما نرخ میانگین موفقیت تاتنهام 1.623 است و نرخ میانگین موفقیت اورتون هم 0.824؛ در نتیجه می توان احتمال گلزنی برای نتیجه موردنظر را حساب کرد).

توزیع پواسون برای بازی تاتنهام و اورتون

این مثال نشان می دهد 19.73 درصد احتمال دارد تاتنهام در گلزنی ناموفق باشد اما 32.02 درصد احتمال دارد آن ها یک گل بزنند و 25.99 درصد احتمال دارد 2 گل بزنند. از سوی دیگر، اورتون 43.86 درصد احتمال دارد در گلزنی ناموفق باشد، 36.14 درصد احتمال دارد 1 گل بزند، 14.89 درصد احتمال دارد 2 گل بزند. آیا امیدی برای این وجود دارد که یک تیم 5 گل بزند؟ احتمال این اتفاق 1.85 درصد برای تاتنهام یا 0.14 درصد برای اورتون است (یا 2 درصد برای هر کدام از تیم ها تا 5 گل بزنند).
تعداد گل های دو تیم دو مفهوم جدا از هم است (از نظر ریاضی) بنابراین می بینید که نتیجه مورد انتظار برای این بازی 1-0 است (با جفت کردن محتمل ترین نتایج برای هر کدام از تیم ها). اگر این دو احتمال را در هم ضرب کنید به احتمال 1-0 شدن بازی می رسید:
0.3202 را در 0.4386 ضرب می کنیم و به عدد 0.1404 می رسیم که یعنی احتمال 14.04 درصد.
حالا شما می دانید چطور احتمالات نتیجه یک بازی را با استفاده از توزیع پواسون محاسبه کنید و از آن در شرط بندی استفاده کنید. در نتیجه می توانید محاسبات خود را با ضریب های یک دلال شرط بندی مقایسه کنید و ببینید آیا اختلافی وجود دارد که از آن بهره مند شوید یا نه. مخصوصا اگر شما در ارزیابی فاکتورهای موقعیتی مربوطه، عواملی مثل آب و هوا و مصدومیت را به عنوان فاکتور جداگانه بررسی کرده باشید.
تبدیل احتمال تخمین زده شده به ضریب
مثال بالا به ما نشان داد که احتمال وقوع نتیجه 1-1 برابر با 11.53 درصد است (0.3202 ضرب در 0.3614). با استفاده از فرمول توزیع پواسون به این رسیدیم. ولی اگر شما بخواهید ضریب های تخمینی برای نتیجه مساوی (به جای تک تک نتایج مساوی احتمالی) در این بازی را بدانید چه کار باید بکنید؟ شما باید احتمال وقوع تمام نتایج مساوی احتمالی را محاسبه کنید: 0-0، 1-1، 2-2، 3-3، 4-4، 5-5 و … .
برای این کار باید احتمال تمام ترکیب های مساوی ممکن را حساب کنید و بعد آن ها را با هم جمع کنید. بدین ترتیب احتمال مساوی شدن نتیجه بازی را به دست می آورید؛ بدون توجه به نتیجه احتمالی.
طبیعتا تعداد نامتناهی احتمال برای مساوی شدن نتیجه بازی وجود دارد (به عنوان مثال ممکن است هر کدام از دو تیم 10 گل بزنند) ولی احتمال وقوع نتیجه مساوی با گل های بیشتر از 5 خیلی کم است و می توان به راحتی آن ها را از این مدل کنار گذاشت.
با استفاده از مثال بازی تاتنهام و اورتون، ترکیب کردن تمام تساوی ها به ما احتمال 0.2472 یا 24.72 درصد را می دهد. بدین ترتیب ضریب درست برای آن هم 4.05 است (0.2472/1).
محدودیت های توزیع پواسون
توزیع پواسون یک مدل پیش بینی ساده است که اجازه نمی دهد از فاکتورهای زیاد استفاده کنیم. در واقع فاکتورهای موقعیتی مثل شرایط باشگاه، شرایط بازی و … و ارزیابی ذهنی تغییر هر کدام از تیم ها در طول پنجره نقل و انتقالات را کاملا نادیده می گیریم.
در این مورد، محاسبات فرمول پواسون نمی تواند تاثیر مربی جدید اورتون (رونالد کومان) روی این بازی را محاسبه کند. در ضمن نمی تواند خستگی احتمالی تاتنهامی ها را وارد محاسبات کند (این بازی نزدیک به بازی قبلی آن ها در رقابت های لیگ اروپاست).
در ضمن ارتباطات همبستگی هم نادیده گرفته شدند؛ مثل فاکتور معروف تاثیر زمین که نشان می دهد در بازی های مشخصی تمایل زیادی به پرگل شدن یا کم گل شدن نتیجه وجود دارد.
این نوع فاکتورها در بازی هایی که در لیگ های سطح پایین انجام می شود مهم تر هستند و می توانند باعث برتری شرط بندها در مقابل دلالان شرط بندی شوند. اما رسیدن به این برتری در بازی های مربوط به لیگ های بزرگ مثل لیگ برتر انگلیس سخت تر است چون دلالان شرط بندی مدرن تخصص و منابع زیادی در اختیار دارند.
در آخر باید به این نکته اشاره کرد که این ضریب ها، کنار گذاشتن هزینه های یک دلال شرط بندی را به عنوان فاکتور جداگانه بررسی نمی کند. این نکته در تمام روند پیداکردن ارزش خیلی مهم است.
بیشتر بخوانید:











دیدگاهتان را بنویسید