سلسله مطالبآموزش پوکرمجله بخت و اقبال،ریاضیات پوکررا بیاموزید.
مفهوم اجرای دوباره (Running it Twice) یا حتی سه باره، بسیار مشهور است. موضوع بسیار ساده است. فرض کنیم 2 نفر در فلاپ حضور دارند. به جای معرفی یک کارت برای ترن و یک کارت برای ریور برای مشخص شدن یک برنده، بازیکنان بین هم توافق می کنند دیلر، کارت های ترن و ریور را دو بار (یا 3 بار) بیرون بکشد. برنده هر کدام از اجراها، نیم یا یک سوم پات (در صورت اجرای سه باره) را مال خود می کند. بازیکنان می توانند هر چند بار که بخواهند، این کار را انجام دهند و در این راه، پات را به تعداد دفعاتی که کارت های جدید رو می شود، تقسیم می کنند.
تنها کاری که اجرای دوباره (یا بیشتر) انجام می دهد، کاهش واریانس (شاخص آماری از نحوه تفاوت نتایج واقعی با نتایج مورد انتظار که در فارسی به عنوان نوسان هم معرفی می شود) کلی شما و ثابت ماندن میزان ارزش مورد انتظارتان (میزان سودآوری یک بازی در بلند مدت) است.
به بیان دیگر، با اجرای دوباره یا بیشتر، نه تنها در بلند مدت، مبلغ برابری به جیب می زنیم، بلکه سرمایه ما در پوکر هم نوسان کمتری به خود می بیند.
چرا ارزش مورد انتظار ثابت می ماند؟
برای درک عمیق تر بعد ریاضی مساله، بهتر است به مثالی ساده نگاه کنیم. فرض کنیم دست قرعه فلاش داریم، ولی به جای دسته کارت کامل:
- فقط 8 کارت باقی مانده
- فقط 2 کارت، فلاش ما را کامل می کند یا به بیان دیگر، تنها 2 آوت داریم
برای سادگی مساله، اول تنها یک بار بازی می کنیم و بعد برای تمام شدن دسته کارت ها، به اجرای چهارم خواهیم رساند. در این حالت، می توانیم اعداد را راحت تر دنبال کنیم و چرایی رفتارشان را درک کنیم. فرضیه هایمان به شرح زیر است:
- بازیکن ما (که از این پس به سبک پوکر هیرو خوانده خواهد شد)، در فلاپ دست قرعه پیک دارد و او تنها در صورتی برنده می شود که فلاش خود را کامل کند
- دسته کارت ها 8 کارت دارد که فقط 2 تای آن ها پیک است
سوال اول: شانس برد دست از سوی هیرو در صورت اجرای تک باره بازی، چقدر است؟
راحت ترین راه برای پاسخ دادن به این سوال، محاسبه سه سناریوی مختلف برد برای هیرو به شرح زیر است:
- او در ترن، موفق می شود و در ریور شکست می خورد: (8/2) * (7/6)= 0.214 یا 21.4 درصد
- او در ترن به کارتش نمی رسد، ولی این کار را در ترن انجام می دهد: (7/2) * (8/6)= 0.214 یا 21.4 درصد (تعجبی هم ندارد. تنها 2 را با 6 عوض کردیم و اینکه هر دو سناریو قرینه هستند)
- هم در ترن و هم در ریور، کارت مورد نظر را به دست آورد: (8/2) * (7/1)= 0.036 یا 3.6 درصد
بنابرین، شانس مجموع برد دست برابر با 21.4+21.4+3.6=46.4 درصد است. البته باید بگوییم این نتیجه بیشتر از آمار واقعی است، چون اینجا فرض کردیم تنها 8 کارت باقی مانده در حالی که در واقعیت 47 کارت باقی می ماند و درصد نهایی بسیار کمتر خواهد بود.
سوال دوم: اگر تمام دسته کارت ها را (برای 4 بار) اجرا کنیم، چه اتفاقی رخ می دهد؟
چون تنها 2 پیک بین کارت ها باقی مانده، 2 مورد خواهیم داشت:
- مورد اول: هیرو در یک چهارم اجراها برنده می شود که به اندازه 25 درصد پات خواهد بود (اگر پیک ها پشت سرهم بیایند)
- مورد دوم: هیرو 2 بار از 4 بار برنده می شود که 50 درصد پات خواهد بود (اگر پیک ها در دسته کارت ها، پراکنده شده باشند)
سوال سوم و نهایی: اگر 4 بار اجرا کنیم، ارزش مورد انتظار هیرو چقدر خواهد بود؟
برای پاسخ دادن به این سوال، باید ببینیم هر کدام از موارد با چه فراوانی رخ می دهد. محاسه فراوانی نسبی مورد اول ساده تر است. قبلا دیدیم رسیدن به هر دو کارت مورد نظر در ترن و ریور، 3.6 درصد موارد رخ می دهد. از این رو، هیرو در هر بار اجرا برای به دست آوردن هر دو پیک، 3.6 درصد شانس دارد:
- 4*3.6=14.4 درصد
بنابرین، مورد اول 14.4 درصد مواقع پیش می آید (25 درصد پات را به هیرو می رساند). به همین ترتیب، باید انتظار داشت مورد دوم 85.6 درصد مواقع رخ داده و نیمی از پات را نصیب هیرو کند. وقتی به شانس ریاضی می رسیم، یک چهارم برابر با 0.25 و نصف برابر با 0.5 است. از این رو، محاسبه ساده نشان می دهد که ارزش مورد انتظار اجرای 4 باره برای هیرو به شرح زیر است:
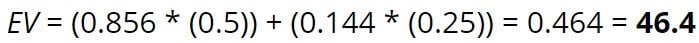
که در آن، ارزش مورد انتظار برابر با 46.4 درصد خواهد بود که دقیقا همان عددی است که در بالا به آن رسیدیم. در نتیجه باید گفت ارزش مورد انتظار هیرو و رقیب در اجراهای زیاد تغییر نمی کند.
نکات مهمی که باید بدانید
در سناریوی بالا، هیرو لایق بدست آوردن 46.6 درصد پات است. با این حال، او هیچ وقت این درصد مشخص را دریافت نمی کند. به جای آن، او یا 50 و یا 25 درصد پات را بدست می آورد. به بیان دیگر، هیرو تنها در 14.4 درصد موارد کمتر از سزاواری اش دریافت می کند. با این حال، با رخداد این موضوع، ضرر بزرگی نصیبش می شود که برابر با 21.4 درصد است:
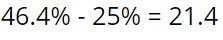
به همین ترتیب، هیرو بیشتر از آن چیزی که سزاورش است دریافت می کند که 85.6 درصد مواقع بوده، ولی میزان بسیار اندکی به شرح زیر نصیبش می شود:
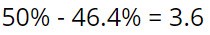
دو نکته آخر مشخص می کند این فرضیه بین بازیکنان پوکر که «موقع داشتن دست قرعه، باید به چند اجرا روی بیاورند»، غلط است. آن ها فکر می کنند شانس بیشتری برای تکه تکه کردن پات دارند. اگر چه بی شک درست است، چیزی که نمی دانند، این است که موقع تکه تکه نشدن پات، آن ها سهم شانس (ارزش مورد انتظار دست یک بازیکن از لحاظ ریاضی در یک دست پوکر، که از طریق ضرب میزان پول موجود در پات در احتمال برد بازیکن محاسبه می شود) اضافه را از دست می دهند.
با اینکه در بالا با سناریویی فرضی روبرو هستیم، ولی برای رقیب، شرطی بدون ریسک تلقی می شود که هیچ گاه ممکن نیست بیشتر از نصف پات را از دست دهد. رقیب اکثر اوقات (85.6 درصد)، سهم شانس را قربانی می کند، ولی می تواند هر از چند گاهی (14.4 درصد)، پات را برای خود نگه داشته و سود بزرگی کند.
همه این ها رخ می دهد و ریسک از دست دادن پات هم وجود ندارد. می توان گفت همه چیز به نفع رقیب است. نکته بالا همچنین منافع اجرای چند باره با توجه به کاهش سود مستمر و واریانس را هم مشخص می کند. به بیان دیگر، هر چه بیشتر اجرا کنیم، به میزان بیشتری به چیزی که استحقاقش را داریم، می رسیم (یا به آن نزدیک می شویم).
مطالب مکمل:












دیدگاهتان را بنویسید